I imagine that anyone who ever played with computer programming at some time or another must have, at least, wondered how they might simulate gravity and a body orbiting the source of that gravity. Now, I am not a blisteringly intelligent chap, but I have a laconic interest in physics, and am saved only (if at all) by the will to learn. For years I shied away from the knitty gritty of this subject of orbits and gravity. It inevitably led to names like Newton, Kepler and Einstein, which filled me - a mere mortal shuffling amongst all the others - with a sense of awe and unattainable knowledge.
Turns out that it is not that difficult to make a very simple 2D orbit simulation. I had a quick search for orbital mechanics, and this result proved valuable...
http://www.arachnoid.com/ruby/gravity/index.html
...particularly the Physics of Gravitation section. I did have a quick scan of the source code, but it was a bit tiresome to follow. Why? I like to code myself, not decipher another’s coding style.
I therefore decided to start from scratch and arm myself only with this reduced formula;
a = G (m/r²)
Feeling like I possessed a blunt gladius before the fire breathing dragon, I concocted a quick C++ model that had Earth's mass. I placed an object at a distance of Earth's radius away from the source of gravity. With some suppression of text output statements and included headers (includes of iostream and math.h, BTW), here it is in essence (drat, how do you indent on a blog?)...
int main(){ const double grav_const = 6.6742e-11; // The "G" in the formula
const double earth_mass = 5.975e24; // The "m" in the formula double radius = 6.37814e6; // The "r" in the formula
double grav_accel = 0; // The "a" in the formula
double vel = 0;
while (radius < 10000)
{
grav_accel = grav_const * (earth_mass / pow(radius, 2)); // The blunt gladius
usleep(1000000); // Pause for a second
vel = vel + grav_accel; // Cause the velocity to be increased each second by
// the gravity acceleration
radius = radius - vel; // Reduce the radius by the velocity each second
}
return 0;
}
Well, it had some error in it, probably due to the abbreviation of the formula, or maybe some imprecision with usleep(). By the way, this is being done with g++ on Gnu/Linux (Debian), so that's the explanation for the appearance of any MSVC/WINAPI unfamiliar functions. Placing the radius at a value equal to Earth's radius should (I believe) cause that radius to decrease to 0 in about 21 minutes. It does so in about 16 minutes in this mock up. First bit of uneasiness there, but once I had a working gravity field I decided to press on.
Here I began to panic. If I wanted an orbit, I would have to figure out a way to calculate the gravitational vectors for a given velocity not parallel to the line between the object and the source of gravity. Keeping in mind that I wanted to start only with a 2D representation, I implemented with the aid of some very simple trigonometry a way to be able to place the attracted body anywhere on a Cartesian 2D grid (X & Y axes) and still have that body attracted directly to the source of gravity.
The arctangent function atan2f(x, y) would provide me the angle and the bog standard Pythagoras formula would give me the radius, adding the following into the main() loop like so;
// The two constants declared above, in the earlier snippet, remain the samedouble radius; // No need to specify the initial radius anymore, it will be calculated in program.double body_x = 2.4e6; // An X axis position of the body to be attracted
double body_y = 7.5e5; // A Y axis position of the body to be attracted
double b_vel_x = 0; // Velocity is now split into two components, X and Y
double b_vel_y = 0; // The original "vel" variable is deleted. double grav_accel = 0;
// At this point in the program I actually stopped using cout from iostream and reverted to
// using the Allegro 5 games programming API to create a timer and graphic representation.
// Read more about Allegro here, if you are interested.// It beats ncurses. If you are an SDL user, then nothing is stopping you, either.
// That is all a bit out of scope of this post, however.
// Now, inside the time interrupt loop, however it is implemented...
// LOOPradius = sqrtf(pow(body_x, 2) + pow(body_y, 2)); // Standard Pythagorasgrav_accel = (grav_const * (earth_mass / pow(radius, 2))); // No changes here
// Here we get the angle of the body to the source of gravity.
// We will need this to compute the grav_accel components on the X and Y axes.
angle = atan2f(body_x, body_y);
// Here we compute the grav_accel components for the X and Y axes, and then
// we add them to the velocity components for each respective axis.b_vel_x += (sin(angle) * (grav_accel));
b_vel_y += (cos(angle) * (grav_accel));
// Finally, we update the X and Y body positions with the velocities...
body_x = body_x - (b_vel_x);
body_y = body_y - (b_vel_y);
// ...and keep looping every second, back up to the LOOP comment.
Well, that worked, but at this point I was somewhat paralyzed, wondering how to incorporate the vectors for non parallel velocities (and how I would even begin to implement Kepler's Second Law), when I had the crazy idea to just go ahead and induce an initial velocity somewhat perpendicular to the gravity vector and see what would happen by simply letting the gravitation formula and velocity components already there deal with it. I expected a monumental failure.
I did this, to the Y axis velocity variable at the declaration point...
double b_vel_y = 12000; // Induce a 12000 m/s velocity
...recompiled and ran it.
Bless those darn "Physicists of Olde" forever. No fictional League of Justice heroes for me, please.
The result was that the body moved initially in the specified Y velocity, and the gravitational acceleration modified this initial velocity into an elliptical orbit around the source of gravity, effectively "capturing" it, just as in "real life".
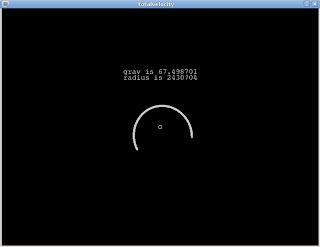
Fig 1:
Screen shot of the "body" being captured in an elliptical orbit. The body is moving counter-clockwise. Exciting, isn't it?
Well I never... How 'bout that? Maybe it is not perfect. Maybe some modern astrophysicists would be moved from their inscrutable heights to sneer or even chuckle at me with some derisive amusement, writhing like an insignificant grub in the moist muck at their feet. But it looked like an orbit to me. Mission accomplished.
Next, get that working in 3D.
HERE IS THE SOURCE CODE FOR A WORKING ALLEGRO5 MODEL OF THIS PROGRAM.
Beautiful work!
ReplyDeleteWith your help I made this,
Using HTML5
Can you post the entire source code? That would be very helpful for me :)
ReplyDeleteSure thing, follow the link at the end of the post. Apologies for the delay in getting back to you, I have not visited my blog for a while. All the best.
DeleteI know this blog post is old, but I wanted to thank you for making this post and also uploading the source code.
ReplyDelete