Gravitational interaction 2D

Back to 2D for simplicity's sake, now. I thought I might play a bit with interactions between bodies of less drastically different masses than, say, a baseball orbiting Earth. That is, I wanted to see a barycenter in action. The classical example of this is the "mutual orbit" of Charon and Pluto.

Now, there's a Newtonian formula that goes into this, but I thought I might take a more grass roots approach to the problem. In my first post, I determined how I might make a body of indeterminate mass (that is; relatively insignificant) orbit around a large mass (like Earth's) with a simplified formula. In this one, I will apply that same formula to a pair of bodies of much similar masses. Charon is 0.116 of Pluto's mass, approximately.

To speed things up a bit, I maintained the masses but shortened the semi major axis. I also upped the time interrupt to 60 frames per second, with each frame counting as a second (ie; time factor X60).

// The variable declarations...
const double grav_const = 6.6742e-11;
const double charon_mass = 1.52e21;
const double pluto_mass = 1.31e22;
double radius;

double charon_x = 2.75e6; // A shortened, arbitrary "axis"
double charon_y = 0;
double charon_vel_x = 0;
double charon_vel_y = 530; // An estimated sample velocity

double pluto_x = 0;
double pluto_y = 0;
double pluto_vel_x = 0;
double pluto_vel_y = -35;

// There is now going to be two separate gravity calculations,
// based on each bodies' mass, each attracting the other.double grav_accel_by_charon = 0;
double grav_accel_by_pluto = 0;

// Each angle could just as easily be done by calculating one and subtracting PI
// from the other, but I am going ahead and calculating each separatelydouble angle_to_charon;
double angle_to_pluto;

// What follows goes inside the time interrupt loop...
angle_to_charon = atan2f((charon_x - pluto_x), (charon_y - pluto_y));
angle_to_pluto = atan2f((pluto_x - charon_x), (pluto_y - charon_y));
radius = sqrtf(pow((charon_x - pluto_x), 2) + pow((charon_y - pluto_y), 2));

grav_accel_by_pluto = (grav_const * (pluto_mass / pow(radius, 2)));
grav_accel_by_charon = (grav_const * (charon_mass / pow(radius, 2)));

charon_vel_x += (sin(angle_to_charon) * grav_accel_by_pluto);
charon_vel_y += (cos(angle_to_charon) * grav_accel_by_pluto);

pluto_vel_x += (sin(angle_to_pluto) * grav_accel_by_charon);
pluto_vel_y += (cos(angle_to_pluto) * grav_accel_by_charon);

charon_x -= charon_vel_x;
charon_y -= charon_vel_y;

pluto_x -= pluto_vel_x;
pluto_y -= pluto_vel_y;

Now that sort of had the desired effect, except that that "Pluto's" counter velocity (-35) was off by a bit. To further complicate the matter, I did not fully calculate the required velocities to make a true circular (non elliptical) orbit of Charon, I just plonked in a rough estimate (530). The result was that, yes, a mutual orbit did occur, but because of unbalanced velocities it crept up the screen as it progressed. In reality, Charon and Pluto are almost perfectly harmonized, Charon having an almost 0 eccentricity around the barycenter. I am not discounting yet that the phenomenon that occurred in my demo can actually happen (screen shots a to c in Figure 3). After all, Charon and Pluto have had, literally, ages to stabilize themselves. I am not going to sit in front of my computer for the next 15 years running this program without interruption to see if my model stabilizes, too. Now, come on! I can, however, dramatically speed up the execution and see what happens, but that some other time. What does seem apparent is that both example are maintaining constant orbits, just that one shifts in space as there is an unbalanced "counter velocity".

For the moment, I just used the "sledge hammer" approach and set the velocities by the respective masses. As Charon is 0.116 of Pluto's mass, I multiplied "my" Charon's velocity (530) and tried that as Pluto's "counter velocity". The results were an improvement (screen shots d to f in Figure 3). The small error is now probably due only to the slight eccentricity.

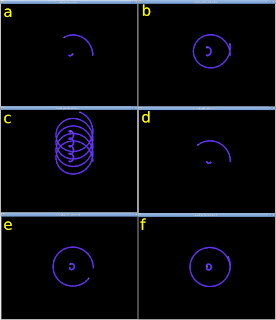
Fig 3: For description, see text above...

Not bad for starters, in any case.

Post Edit: Hmmm. I do now think there is something not right, however. Look what I just found. That is more or less what I am aiming at.