Final polish to the Naval Gun

And now I want to study that interpolation function, so I have reference to return to in case I forget (again) how I did it. What happens?

double ref_Mach_table[MACH_CD_ELEMENTS] =
{-0.10, 0.00, 0.40, 0.60, 0.87, 1.02, 1.15, 2.40, 3.40};

double ref_Cd_table[MACH_CD_ELEMENTS] =
{0.000, 0.231, 0.229, 0.172, 0.139, 0.333, 0.341, 0.268, 0.255};

//............

double Cd_Calculator(double Mach)
{
int index_count;

for(index_count = 0; index_count < MACH_CD_ELEMENTS; index_count++)
{
if(ref_Mach_table[index_count] > Mach)
break;
}

double inter_factor =
(Mach - ref_Mach_table[index_count - 1]) / (ref_Mach_table[index_count] - ref_Mach_table[index_count - 1]);

double output =
((ref_Cd_table[index_count] - ref_Cd_table[index_count - 1]) * inter_factor) + ref_Cd_table[index_count - 1];

return output;
}

The function is called using the calculated Mach number as the parameter. The for loop counts up (increasing the index_count) until the value in the Mach table (the ref_Mach_table array element of the index_count) exceeds the value of the passed Mach number, then breaks out with the corresponding index_count.

The range of the table values, the upper and the lower, that enclose the passed Mach value is then calculated;

ref_Mach_table[index_count] - ref_Mach_table[index_count - 1]

For example, a value of Mach 1.9 is passed. That being between 2.40 and 1.15, the formula will calculate the Mach range of;

2.40 - 1.15 = 1.25

Then the difference of the passed Mach value from the lower table value is calculated;

1.9 - 1.15 = 0.75

Then, in coefficient (percentage, if you like) of the relation of the relation of the true difference to the available table range is calculated;

0.75 / 1.25 = 0.6

And that is the interpolation factor for the ref_Cd_table array, and what is happening in the line that calculates inter_factor. I am just doing a straight forward linear interpolation here, by the way. Armed with inter_factor and index count, I then move to the ref_Cd_table and find the range of the two Cd values that correspond to the index_count and index_count - 1.

ref_Cd_table[index_count] - ref_Cd_table[index_count - 1]

These values are 0.268 and 0.341. So we get;

0.268 - 0.341 = -0.073

A negative value, as the Cd is reducing with increase in Mach at these velocities. I multiply that by the inter_factor to get what the Cd change is between the two Cd table values at 0.6 (60%) between them.

0.6 x -0.073 = -0.0438

I now add that to the Cd value that corresponds to the [index_count - 1] element, which is 0.341;

0.341 + -0.0438 = 0.2972

And that is the new interpolated Cd returned by the function (result of the computations for the variable output). This is the Cd value that gets passed to the drag calculation formula.

Now, finally, a refinement of the drag calculations by obtaining the air density at the shell's altitude. As air density reduces with increasing altitude, the shell is going to be traveling through a less dense medium at the top of its trajectory. I believe it was this ship, that ended her days as a war trophy and was subjected to nuclear bomb tests at Kwajalein atoll, that had high elevation guns (37º, where most maximum elevations were in the region of 25º to 30º), which greatly enhanced the fighting capabilities of the already formidable 8" main weapon by sending the shell high into the lower density atmosphere.

I got the density ratios for ISA out of a book I have, Aerodynamics for Naval Aviators, though I am sure it can be found also with a good internet search.

const int REF_RHO_ELEMENTS = 12;

double ref_rhos[REF_RHO_ELEMENTS] =
{1.000, 0.8617, 0.7385, 0.6292, 0.5328, 0.4481, 0.3741, 0.3099, 0.2462, 0.1936, 0.1522, 0.1197};
// These are percentage values of the air density, relative to the SL density of 1.225 kg/m³
// The resolution of the density ratio is for every 1525 meters.

// Related declarations...
double rho_gradient = 1525; // Meters
double actual_rho;

double Rho_Calculator(double altitude, double gradient, double sl_rho)
{
double alt_ref = altitude / gradient;
// Eg; 1872 / 1525 = 1.227541

int index_count = int(alt_ref);
// Eg; int(1.227541) = 1. This is the index position in ref_rhos[]
// As this is a constant increment of altitude gradient,
// the interpolation factor is pretty direct, as in;

double inter_factor = alt_ref - index_count;

double rho_coeff =
((ref_rhos[index_count + 1] - ref_rhos[index_count]) * inter_factor) + ref_rhos[index_count];

return sl_rho * rho_coeff;
}

This is actually a simpler interpolation than the previous, as it does not have a variable primary interpolation range, as the first one did. The altitude increments are constant, and only the density ratio lapse relaxes with increasing altitude. It is fairly self explanatory. It is called, BEFORE the drag calculation, like this...

actual_rho = Rho_Calculator(ypos, rho_gradient, ISA_Rho);

And the drag calculation, to recap, looks like this...

double Velocity_Calculator(double vel, double mass, double rho, double d_coeff, double FA)
{
double energy = vel * mass;
double drag = 0.5 * rho * pow(vel, 2) * d_coeff * FA;
energy -= drag;
return energy / mass;
}

Note that I now have it as a separate function, called from inside the update loop, after all the Rho and Mach calculations are done, like this...

velocity =
Velocity_Calculator(velocity, mass_kg, actual_rho, Cd, frontal_area);

That would be all, for now.

More for the Naval Gun

As the title says, a bit more for the Naval Gun. I am going to do this in a couple of posts, to keep it in bite sized portions. Ballistics, especially of a spinning shell, is a complex, 3 dimensional arena. This model is limited to 2D for the moment. The day may come when I decide to tackle precession induced drift. For the moment, I just want to make this one, as it is, a bit more credible. One of the features of a naval shell, as fired from those magnificent warships of World War I and II, was that they were supersonic, a while before aircraft broke the legendary "sound barrier".

One of the notable traits of approaching "the speed of sound" is that the behavior of drag changes. There is a sharp increase in drag through the transonic region, and then a gradual fall off of this increased drag as the body accelerates beyond the speed of sound. This behavior is best represented, in a simulator model, by making the Coefficient of Drag a variable, the value of which is dependent upon the shell's velocity in relation to Mach 1. In my previous model, Cd was a fixed value. This was okay for starters, but it is NOT correct.

Now, things get a bit more intricate. The speed of sound is itself dependent on the atmospheric temperature. If you are a pilot, or even a dedicated "simmer", you will probably have an ARC-1 or E6B Flight Computer. There is a little scale on the computer side, where you match up a temperature to an M symbol, and read off the speed of an equivalent Mach number from the inner scale to knots on the outer scale. As a rough guide, a velocity of 340.278 m/s is equivalent to Mach 1 at 15º C (International Standard Atmosphere at Sea Level). And every drop of 1º C incurs a reduction of Mach 1 equivalent velocity by 0.61 m/s, approximately. So, if the temperature is 12º C, then Mach 1 is equivalent to;

340.278 - ((15 - 12) * 0.61)

To get the Mach number from this, divide the actual velocity of the shell (in m/s) by the corresponding Mach 1, in m/s, obtained for the given temperature.

Mach_Number_of_Shell = Velocity_of_Shell_ms / Velocity_of_Mach_1_ms

And that, basically, is what I am going to do with my model as a required step in determining a variable Coefficient of Drag. The temperature drops at an environmental lapse rate of 1º C per every 152.39 meters gained.

Declarations first, with all the others;

double ISA_temp_C = 15;
double temp_meters_degree_C = 152.39; // Meters of altitude per every -1º C
double ref_Mach_1 = 340.278; // Meters per second at 15º C
double Mach_fall_off = 0.61; // Mach meters per second less per every -1º C
double velocity_Mach;

Now, I decided to make a small function that I would call from inside the update loop. Here it is;

double Mach_Calculator(double altitude, double SL_temp, double alt_temp_lapse, double ref_M1, double Mach_lapse, double vel)
{
double temp_at_alt = SL_temp - (altitude / alt_temp_lapse);
double Mach_1_at_alt = ref_M1 - ((SL_temp - temp_at_alt) * Mach_lapse);
return vel / Mach_1_at_alt;
}

And that was it, in the simplest terms. I now have the shell velocity expressed in Mach number. I call the function with these parameters;

velocity_Mach =
Mach_Calculator(ypos, ISA_temp_C, temp_meters_degree_C, ref_Mach_1, Mach_fall_off, velocity);

Onwards. Now let's go get that variable Coefficient of Drag. There are (very complicated) ways of computing Cd. I opted for an easy way out, at this stage. Check out this page. Down on the Doppler Radar-measurements section, there is a model of a bullet's coefficient of drag at different Mach velocities. I mapped something like that into two arrays, declared globally, in my program, like this;

const int MACH_CD_ELEMENTS = 9;

double ref_Mach_table[MACH_CD_ELEMENTS] =
{-0.10, 0.00, 0.40, 0.60, 0.87, 1.02, 1.15, 2.40, 3.40};

double ref_Cd_table[MACH_CD_ELEMENTS] =
{0.000, 0.231, 0.229, 0.172, 0.139, 0.333, 0.341, 0.268, 0.255};

Simply matched up some Mach numbers (first array) to some Cd values (second array. Now it will just be a case of using the computed Mach velocity of the shell to find a corresponding Cd. So, it is all very well to say, looking at the two arrays, that if the shell is traveling at Mach 1.15, then the Cd is 0.341 (both being the seventh element in their respective arrays), but what if the shell is doing Mach 1.95? The Cd value is somewhere between 0.341 and 0.268. We need to interpolate. Here's the function that does it...

double Cd_Calculator(double Mach)
{
int index_count;

for(index_count = 0; index_count < MACH_CD_ELEMENTS; index_count++)
{
if(ref_Mach_table[index_count] > Mach)
break;
}

double inter_factor =
(Mach - ref_Mach_table[index_count - 1]) / (ref_Mach_table[index_count] - ref_Mach_table[index_count - 1]);

double output =
((ref_Cd_table[index_count] - ref_Cd_table[index_count - 1]) * inter_factor) + ref_Cd_table[index_count - 1];

return output;
}

So, what's it doing? That's the subject of the next post, where I will also interpolate to get a variable atmospheric density at different altitudes, adding a bit more polish to the model. For the moment, this function gets called AFTER determining the Mach number and BEFORE calculating the drag (in the update loop), like this...

Cd = Cd_Calculator(velocity_Mach);

That's already improved the model. It now has a variable Coefficient of Drag, dependent on the Mach number, which is in turn dependent on the shell velocity at different air temperatures.

Naval Gun

And now a brief intermission from all that "space stuff". I thought I might tackle the challenge of modeling a ballistic trajectory of a 15" naval gun, as used on this ship, for example. Now there are a couple of factors that influence the trajectory of a projectile of a given velocity; gravity and drag.

Gravity I have already looked into in my previous posts. For this model, fired in a local area on the surface of the Earth, the variations in its acceleration would be negligible, so I established it constant at 9.807 m/s². At this point I will just go ahead and plot a trajectory without drag (air resistance) to see what I get.

Apart from the gravity, I established some initial data for the calculation. They would be shell velocity (initial, or muzzle velocity if you like), and angle (elevation) of the gun, so that it fires upwards like a mortar shot, the way it did, and loft the shell off towards its target in the distance. Here's how the program started off (I am not going to do that complete color formatting anymore, it is a pain. From now, comments are going to be pale blue, code in dark blue);

int main()
{
// variable declarations...
double grav_accel = 9.807;
double velocity = 785; // meters per second
double xpos = 0, ypos = 0; // The shell positions, each unit a meter.
double xvel, yvel; // The shell X and Y (2D) velocity components.
double angle = 0.40; // Angle in radians, approximately 23º.
// For the record (I am always mixing this up)....
// To convert radians to degrees, first divide them by PI, then multiply by 180.
// To convert degrees to radians, first divide them by 180, then multiply by PI.

// Code continues after the following comment....

Once that is established, we can set up a loop to move the shell. The thing to consider here is that during the upward travel of the shell, gravity is going to slow its velocity on the Y component (vertical). This will slowly alter the trajectory, as it will also slow its total velocity. And on the "way down" gravity will increase the projectile velocity (drag being nonexistent, to start with. Later we will see how drag affects this).

This is what needs to be calculated.

// Code continues here...

while(ypos >= 0) // While the shell is above the "ground", or "sea", as it were.
{
xvel = cos(angle) * velocity;
yvel = sin(angle) * velocity;

xpos += xvel;
ypos += (yvel - grav_accel);

velocity = sqrt(pow(xvel, 2) + pow((yvel - grav_accel), 2));
angle = atan2f((yvel - grav_accel), xvel);

usleep(1000000);
}
return 0;
}

At first glance it may appear that there is a bit much there. Why not just compute the vertical velocity component and leave it at that? There would be no change to the horizontal component of the velocity as it changed its trajectory, which is what really happens. That is why. As the shell travels upwards, a component of gravity is subtracting velocity from the shell's total velocity.

For example, if the code were left simply as...

xvel = cos(angle) * velocity;
yvel = sin(angle) * velocity;

xpos += xvel;
ypos += (yvel - grav_accel);

...and looped through as that, the horizontal velocity would always be the result of Cos(angle) x velocity (ie; Cos(22º) x 785 = 727.8 m/s). This would extend the range of the gun unrealistically, as there would be no degradation of its velocity caused by it "fighting its way uphill" at the beginning of its trajectory. The new velocity is calculated by invoking Pythagoras with the new components of X and Y velocity. Then the new angle of the resultant trajectory is also calculated from the new components (atan()), and that data is fed back into the loop. The program will run as it is, now.

However, that is not the end of the story. The shell travels through the atmosphere, and the atmosphere has a density that causes aerodynamic drag. The formula for drag is;

Drag = 0.5 x Velocity² x Air_Density x Drag_Coefficient x Frontal_Area

In SI units, that would give you the force of drag in Newtons (I believe. Most of my usage of lift and drag formula in the past have been in Imperial units, which provides the force in pounds. This is the first time I am applying it with SI units). So, now I needed to supply some more data to the program in order to calculate this. Velocity we already have, so we add to the variable declarations the following;

double frontal_area = 0.1148; // m², about the frontal area of a 15 inch diameter shell.
double Cd = 0.22; // An estimated, "probable" coefficient of drag.
double Rho = 1.225; // kg/m³, air density, according to SL ISA.
double drag;

All very well, but now the drag has to "work" against something. That "something" would be the momentum (inertia) of a shell of a certain mass traveling at a certain velocity. Here is where I get a bit "plauged" by doubt, but I do believe that I am correct in stating that the motion inertia of the shell is equivalent to its mass multiplied by its velocity. Let's call it "momentum" for the moment, to differentiate it from kinetic energy, which is a different formula (and provides preposterously large results for the purpose of this model). The unit of the product would be the Kg Meter per Second (Newton Second). I add these two more variables to the declarations in the code;

double mass = 870; // kg
double momentum;

And now to the calculations. This would go inside the loop, in the code above, just after the angle calculation and before the usleep() function call.

drag = 0.5 * Rho * pow(velocity, 2) * Cd * frontal_area;
momentum = (velocity * mass) - drag; // I believe the units are compatible here.
// At least, the results of the running program are quite acceptable.

velocity = momentum / mass;
// From the energy, devise the new velocity, and then loop back to the beginning,
// armed with the new trajectory angle and shell velocity.

It might not be perfect, but the output (which can be seen by adding some cout statements to the code) is actually quite convincing. There is a slight excess of range, but I believe it might be because the Cd is a tad low. After all, it was only estimated. The shell goes up almost 4 km, travels 29 km, taking 55 seconds to do so, and arrives at the target at a velocity of about 480 m/s, having decelerated from its original 785 m/s, and been at about 540 m/s at the top of the trajectory. These figures are not far off the performance of the real gun.

After note:
I had some fun with this one. Obviously, the code can be cleaned up, or neatly packaged away in a function, but the basic idea is there. A couple of members of a naval history forum provided me with some additional sources of information (data) on gun ranges and trajectories. I really was not far off, at all, except that it is closer to the real performance of the gun if the coefficient of drag is raised to 0.25 or 0.26, instead of 0.22.

'Till the next installment!

More on Barycenters

Picking up a bit where I left off. According to someone with a Phd on a forum that knows a great deal about astrophysics, there was absolutely nothing wrong with my rendition of a barycenter orbit. The shifting of the barycenter if no "counter velocity" is established for the more massive body will occur because momentum must be conserved. Makes sense.

Anyway, here is a representation of the same barycenter orbit, the white one leaving the visual representation (the frame of reference) as it is, the orange one "correcting" the positions so that it appears that the more massive body is "stationary". It is a visual trick, they are really the same orbit.



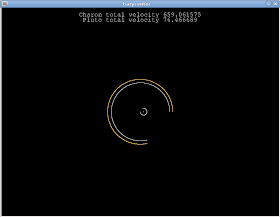
And here's the "correcting" code.

barycenter_length = radius * (charon_mass / (charon_mass + pluto_mass));
bary_x = sin(angle_to_charon) * barycenter_length;
bary_y = cos(angle_to_charon) * barycenter_length;

Then, this code keeps the more massive body centered...

pluto_x + bary_x
pluto_y + bary_y

And so on for Charon. That is, by the way, the formula for establishing a barycenter;

Bc = Radius * (lesser_mass / (lesser_mass + greater_mass))

I am sort of up to my eyes in work this month, so progress will be slow.

'Till the next!

Gravitational interaction 2D

Back to 2D for simplicity's sake, now. I thought I might play a bit with interactions between bodies of less drastically different masses than, say, a baseball orbiting Earth. That is, I wanted to see a barycenter in action. The classical example of this is the "mutual orbit" of Charon and Pluto.

Now, there's a Newtonian formula that goes into this, but I thought I might take a more grass roots approach to the problem. In my first post, I determined how I might make a body of indeterminate mass (that is; relatively insignificant) orbit around a large mass (like Earth's) with a simplified formula. In this one, I will apply that same formula to a pair of bodies of much similar masses. Charon is 0.116 of Pluto's mass, approximately.

To speed things up a bit, I maintained the masses but shortened the semi major axis. I also upped the time interrupt to 60 frames per second, with each frame counting as a second (ie; time factor X60).

// The variable declarations...
const double grav_const = 6.6742e-11;
const double charon_mass = 1.52e21;
const double pluto_mass = 1.31e22;
double radius;

double charon_x = 2.75e6; // A shortened, arbitrary "axis"
double charon_y = 0;
double charon_vel_x = 0;
double charon_vel_y = 530; // An estimated sample velocity

double pluto_x = 0;
double pluto_y = 0;
double pluto_vel_x = 0;
double pluto_vel_y = -35;

// There is now going to be two separate gravity calculations,
// based on each bodies' mass, each attracting the other.double grav_accel_by_charon = 0;
double grav_accel_by_pluto = 0;

// Each angle could just as easily be done by calculating one and subtracting PI
// from the other, but I am going ahead and calculating each separatelydouble angle_to_charon;
double angle_to_pluto;

// What follows goes inside the time interrupt loop...
angle_to_charon = atan2f((charon_x - pluto_x), (charon_y - pluto_y));
angle_to_pluto = atan2f((pluto_x - charon_x), (pluto_y - charon_y));
radius = sqrtf(pow((charon_x - pluto_x), 2) + pow((charon_y - pluto_y), 2));

grav_accel_by_pluto = (grav_const * (pluto_mass / pow(radius, 2)));
grav_accel_by_charon = (grav_const * (charon_mass / pow(radius, 2)));

charon_vel_x += (sin(angle_to_charon) * grav_accel_by_pluto);
charon_vel_y += (cos(angle_to_charon) * grav_accel_by_pluto);

pluto_vel_x += (sin(angle_to_pluto) * grav_accel_by_charon);
pluto_vel_y += (cos(angle_to_pluto) * grav_accel_by_charon);

charon_x -= charon_vel_x;
charon_y -= charon_vel_y;

pluto_x -= pluto_vel_x;
pluto_y -= pluto_vel_y;

Now that sort of had the desired effect, except that that "Pluto's" counter velocity (-35) was off by a bit. To further complicate the matter, I did not fully calculate the required velocities to make a true circular (non elliptical) orbit of Charon, I just plonked in a rough estimate (530). The result was that, yes, a mutual orbit did occur, but because of unbalanced velocities it crept up the screen as it progressed. In reality, Charon and Pluto are almost perfectly harmonized, Charon having an almost 0 eccentricity around the barycenter. I am not discounting yet that the phenomenon that occurred in my demo can actually happen (screen shots a to c in Figure 3). After all, Charon and Pluto have had, literally, ages to stabilize themselves. I am not going to sit in front of my computer for the next 15 years running this program without interruption to see if my model stabilizes, too. Now, come on! I can, however, dramatically speed up the execution and see what happens, but that some other time. What does seem apparent is that both example are maintaining constant orbits, just that one shifts in space as there is an unbalanced "counter velocity".

For the moment, I just used the "sledge hammer" approach and set the velocities by the respective masses. As Charon is 0.116 of Pluto's mass, I multiplied "my" Charon's velocity (530) and tried that as Pluto's "counter velocity". The results were an improvement (screen shots d to f in Figure 3). The small error is now probably due only to the slight eccentricity.

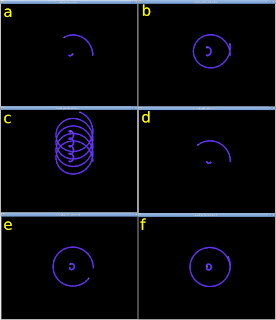
Fig 3: For description, see text above...

Not bad for starters, in any case.

Post Edit: Hmmm. I do now think there is something not right, however. Look what I just found. That is more or less what I am aiming at.

Simple 3D Orbit

This is, therefore, the next logical extension to the previous post. Here I tackle the problem of establishing an orbit with coordinates in X, Y and Z axes. In a way, the three axes already exist to an extent even in the 2D version. It is quite important to realize that, as it makes the transition to 3D much easier if you are aware of it. How? In the 2D version, the coordinates of the body are mapped on the X and Y axes (across and down the screen), but the representation of the orbit rotates around the Z axis (perpendicular to the screen's surface, out of it).

The rotation axis for mapping the X and Y coordinates remains the same (around the Z axis), and the rotation axis for mapping the new Z coordinate becomes the "pseudo axis" (let's call it that) formed by the line from the origin (0, 0) to the body's X and Y coordinates. By those means, you only need to compute 2 angles to establish points in 3D. Those angles are azimuth and elevation. As we are not doing any "local" rotations of the body itself, these suffice.

A bit more on this here, for example; MathTeacher

Down to it, then. These are the new variables (excluding those we know should be there, by now; gravitational constant and mass).

double radius_1;
double radius_2;
double body_x = 1.5e6;
double body_y = 6.5e5;
double body_z = 7.5e5;
double b_vel_x = 0;
double b_vel_y = 3000;
double b_vel_z = 12000;
double grav_accel = 0;
double angle_1;
double angle_2;

// Here we do what we have done all along, except now they are known as angle_1 and radius_1
angle_1 = atan2f(body_x, body_y);
radius_1 = sqrtf(pow(body_x, 2) + pow(body_y, 2));

// We then use radius_1 with the body_z coordinate to obtain the elevation angle (ie; angle_2)
angle_2 = atan2f(body_z, radius_1);

// Now, obtain the total length of the bona fide 3D radius.
radius_2 = sqrtf(pow(body_x, 2) + pow(body_y, 2) + pow(body_z, 2));

// and the gravitation along the 3D radius.
grav_accel = (grav_const * (earth_mass / pow(radius_2, 2)));

// Now, the velocites produced by the gravity field...
// For the X and Y axes, they are "shortened" by the cosine of the elevation angle
// For the Z axis, it is simply the sine of the elevation angle
// Remember, the elevation angle was already taken from an axis (mostly) neither
// parallel to the X or Y axis.
b_vel_x = b_vel_x + ((sin(angle_1) * cos(angle_2)) * (grav_accel ));
b_vel_y = b_vel_y + ((cos(angle_1) * cos(angle_2)) * (grav_accel ));
b_vel_z = b_vel_z + (sin(angle_2) * (grav_accel ));

// And affect the respective velocities to the body coordinates.
body_x = body_x - (b_vel_x);
body_y = body_y - (b_vel_y);
body_z = body_z - (b_vel_z);

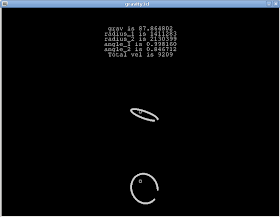
Fig 2:
A 3D elliptical orbit closing. Upper view is X, Y axes plan, lower view is X, Z axes plan.

Simple 2D Orbit

I imagine that anyone who ever played with computer programming at some time or another must have, at least, wondered how they might simulate gravity and a body orbiting the source of that gravity. Now, I am not a blisteringly intelligent chap, but I have a laconic interest in physics, and am saved only (if at all) by the will to learn. For years I shied away from the knitty gritty of this subject of orbits and gravity. It inevitably led to names like Newton, Kepler and Einstein, which filled me - a mere mortal shuffling amongst all the others - with a sense of awe and unattainable knowledge.

Turns out that it is not that difficult to make a very simple 2D orbit simulation. I had a quick search for orbital mechanics, and this result proved valuable...

http://www.arachnoid.com/ruby/gravity/index.html

...particularly the Physics of Gravitation section. I did have a quick scan of the source code, but it was a bit tiresome to follow. Why? I like to code myself, not decipher another’s coding style.

I therefore decided to start from scratch and arm myself only with this reduced formula;

a = G (m/r²)

Feeling like I possessed a blunt gladius before the fire breathing dragon, I concocted a quick C++ model that had Earth's mass. I placed an object at a distance of Earth's radius away from the source of gravity. With some suppression of text output statements and included headers (includes of iostream and math.h, BTW), here it is in essence (drat, how do you indent on a blog?)...

int main(){ const double grav_const = 6.6742e-11; // The "G" in the formula
const double earth_mass = 5.975e24; // The "m" in the formula double radius = 6.37814e6; // The "r" in the formula
double grav_accel = 0; // The "a" in the formula
double vel = 0;

while (radius < 10000)
{
grav_accel = grav_const * (earth_mass / pow(radius, 2)); // The blunt gladius
usleep(1000000); // Pause for a second
vel = vel + grav_accel; // Cause the velocity to be increased each second by
// the gravity acceleration
radius = radius - vel; // Reduce the radius by the velocity each second
}
return 0;
}
Well, it had some error in it, probably due to the abbreviation of the formula, or maybe some imprecision with usleep(). By the way, this is being done with g++ on Gnu/Linux (Debian), so that's the explanation for the appearance of any MSVC/WINAPI unfamiliar functions. Placing the radius at a value equal to Earth's radius should (I believe) cause that radius to decrease to 0 in about 21 minutes. It does so in about 16 minutes in this mock up. First bit of uneasiness there, but once I had a working gravity field I decided to press on.

Here I began to panic. If I wanted an orbit, I would have to figure out a way to calculate the gravitational vectors for a given velocity not parallel to the line between the object and the source of gravity. Keeping in mind that I wanted to start only with a 2D representation, I implemented with the aid of some very simple trigonometry a way to be able to place the attracted body anywhere on a Cartesian 2D grid (X & Y axes) and still have that body attracted directly to the source of gravity.

The arctangent function atan2f(x, y) would provide me the angle and the bog standard Pythagoras formula would give me the radius, adding the following into the main() loop like so;

// The two constants declared above, in the earlier snippet, remain the samedouble radius; // No need to specify the initial radius anymore, it will be calculated in program.double body_x = 2.4e6; // An X axis position of the body to be attracted
double body_y = 7.5e5; // A Y axis position of the body to be attracted
double b_vel_x = 0; // Velocity is now split into two components, X and Y
double b_vel_y = 0; // The original "vel" variable is deleted. double grav_accel = 0;

// At this point in the program I actually stopped using cout from iostream and reverted to
// using the Allegro 5 games programming API to create a timer and graphic representation.
// Read more about Allegro here, if you are interested.// It beats ncurses. If you are an SDL user, then nothing is stopping you, either.
// That is all a bit out of scope of this post, however.
// Now, inside the time interrupt loop, however it is implemented...
// LOOPradius = sqrtf(pow(body_x, 2) + pow(body_y, 2)); // Standard Pythagorasgrav_accel = (grav_const * (earth_mass / pow(radius, 2))); // No changes here

// Here we get the angle of the body to the source of gravity.
// We will need this to compute the grav_accel components on the X and Y axes.
angle = atan2f(body_x, body_y);
// Here we compute the grav_accel components for the X and Y axes, and then
// we add them to the velocity components for each respective axis.b_vel_x += (sin(angle) * (grav_accel));
b_vel_y += (cos(angle) * (grav_accel));

// Finally, we update the X and Y body positions with the velocities...
body_x = body_x - (b_vel_x);
body_y = body_y - (b_vel_y);

// ...and keep looping every second, back up to the LOOP comment.
Well, that worked, but at this point I was somewhat paralyzed, wondering how to incorporate the vectors for non parallel velocities (and how I would even begin to implement Kepler's Second Law), when I had the crazy idea to just go ahead and induce an initial velocity somewhat perpendicular to the gravity vector and see what would happen by simply letting the gravitation formula and velocity components already there deal with it. I expected a monumental failure.

I did this, to the Y axis velocity variable at the declaration point...

double b_vel_y = 12000; // Induce a 12000 m/s velocity

...recompiled and ran it.

Bless those darn "Physicists of Olde" forever. No fictional League of Justice heroes for me, please.

The result was that the body moved initially in the specified Y velocity, and the gravitational acceleration modified this initial velocity into an elliptical orbit around the source of gravity, effectively "capturing" it, just as in "real life".

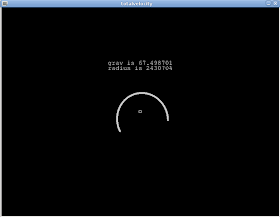
Fig 1:
Screen shot of the "body" being captured in an elliptical orbit. The body is moving counter-clockwise. Exciting, isn't it?

Well I never... How 'bout that? Maybe it is not perfect. Maybe some modern astrophysicists would be moved from their inscrutable heights to sneer or even chuckle at me with some derisive amusement, writhing like an insignificant grub in the moist muck at their feet. But it looked like an orbit to me. Mission accomplished.

Next, get that working in 3D.

HERE IS THE SOURCE CODE FOR A WORKING ALLEGRO5 MODEL OF THIS PROGRAM.